Pembahasan Matematika Ipa Un 2013 No. 11 - 15

Pembahasan soal-soal Ujian Nasional (UN) tahun 2013 bidang studi Matematika SMA-IPA nomor 11 hingga dengan nomor 15 tentang:
- komposisi fungsi,
- invers fungsi,
- program linear,
- matriks, dan
- operasi vektor.
Soal No. 11 perihal Komposisi Fungsi
Diketahui fungsi f(x) = x − 4 dan g(x) = x2 − 3x + 7. Fungsi komposisi (g ∘ f)(x) = ….
A. x2 − 3x + 3
B. x2 − 3x + 11
C. x2 − 11x + 15
D. x2 − 11x + 27
E. x2 − 11x + 35
A. x2 − 3x + 3
B. x2 − 3x + 11
C. x2 − 11x + 15
D. x2 − 11x + 27
E. x2 − 11x + 35
Pembahasan
Perhatikan fungsi komposisi yang ditanyakan!(g ∘ f)(x) = g[f(x)]
Letak fungsi g ada di depan sehingga kita harus berpatokan pada fungsi g(x).
g(x) = x2 − 3x + 7
g[f(x)] = [f(x)]2 − 3f(x) + 7
= (x − 4)2 − 3(x − 4) + 7
= x2 − 8x + 16 − 3x + 12 + 7
= x2 − 11x + 35
Jadi, fungsi komposisi (g ∘ f)(x) ialah opsi x2 − 11x + 35 (E).
Perdalam bahan ini di Pembahasan Matematika IPA UN: Komposisi dan Invers Fungsi
Soal No. 12 perihal Invers Fungsi
Diketahui fungsi
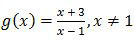
Invers fungsi g ialah g−1(x) = ….
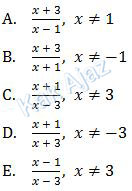
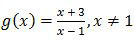
Invers fungsi g ialah g−1(x) = ….
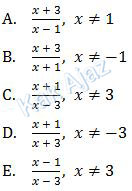

Pembahasan
Invers fungsi bagian linear dirumuskan: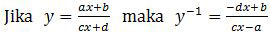
Berdasarkan rumus di atas maka:

Jadi, Invers fungsi g ialah opsi (A).
Perdalam bahan ini di Pembahasan Matematika IPA UN: Komposisi dan Invers Fungsi
Soal No. 13 perihal Program Linear
Luas kawasan parkir 1.760 m2. Luas rata-rata untuk kendaraan beroda empat kecil 4 m2 dan kendaraan beroda empat besar 20 m2. Daya tampung maksimum hanya 200 kendaraan. Biaya parkir kendaraan beroda empat kecil Rp1.000,00/jam dan kendaraan beroda empat besar Rp2.000,00/jam. Jika dalam satu jam terisi penuh dan tidak ada kendaraan yang pergi dan datang, penghasilan maksimum tempat parkir ialah ….
A. Rp176.000,00
B. Rp200.000,00
C. Rp260.000,00
D. Rp300.000,00
E. Rp340.000,00
A. Rp176.000,00
B. Rp200.000,00
C. Rp260.000,00
D. Rp300.000,00
E. Rp340.000,00
Pembahasan
buat tabel tunjangan untuk soal di atas.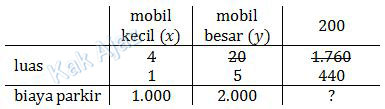
Berdasarkan tabel tunjangan di atas, diperoleh:
- x + y = 200 … (1)
- x + 5y = 440 … (2)
- Fungsi objektif z = 1.000x + 2.000y
x + y = 200
x + 5y = 440
⎯⎯⎯⎯⎯⎯⎯⎯ − [bawah dikurangi atas]
4y = 240
y = 60
Selanjutnya kita substitusi y = 60 ke persamaan (1).
x + y = 200
x + 60 = 200
x = 140
Dengan demikian, nilai fungsi objektif adalah:
z = 1.000x + 2.000y
= 1.000 × 140 + 2.000 × 60
= 140.000 + 120.000
= 260.000
Jadi, penghasilan maksimum tempat parkir tersebut ialah Rp260.000,00 (C).
Perdalam bahan ini di Pembahasan Matematika IPA UN: Program Lnear
Soal No. 14 perihal Matriks
Diketahui persamaan matriks
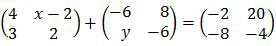
Nilai dari x + y = ….
A. 3
B. 11
C. 14
D. 19
E. 25
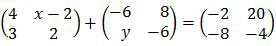
Nilai dari x + y = ….
A. 3
B. 11
C. 14
D. 19
E. 25
Pembahasan
Agar lebih efektif, operasikan komponen matriks yang mengandung variabel saja, yaitu kanan atas dan kiri bawah.- Kanan atas
x − 2 + 8 = 20
x + 6 = 20
x = 14
- Kiri bawah
3 + y = −8Dengan demikian,
y = −11
x + y = 14 − 11
= 3
Jadi, nilai dari x + y ialah 3 (A).
Perdalam bahan ini di Pembahasan Matematika IPA UN: Matriks
Soal No. 15 perihal Operasi Vektor
Diketahui vektor a = 2i − j, b = 2i − k, dan c = 3i + j + 2k. Hasil a + 2b − c ialah ….
A. −i + 2j − 4k
B. 5i − 3j
C. i − 2j + 2k
D. i − 3j + 4k
E. i − 2j + 4k
A. −i + 2j − 4k
B. 5i − 3j
C. i − 2j + 2k
D. i − 3j + 4k
E. i − 2j + 4k
Pembahasan
Operasi vektor-vektor di atas akan terkesan lebih gampang dikerjakan kalau dinotasikan dalam bentuk kolom.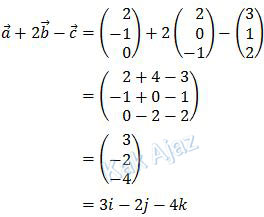
Jadi, hasil a + 2b − c ialah 3i − 2j − 4k (-).
Perdalam bahan ini di Pembahasan Matematika IPA UN: Operasi Vektor
Pembahasan Matematika IPA UN 2013 No. 6 - 10
Pembahasan Matematika IPA UN 2013 No. 16 - 20
Dapatkan pembahasan soal dalam file pdf di sini.
Demikian, menyebarkan pengetahuan bersama . Silakan bertanya di kolom komentar apabila ada pembahasan yang kurang jelas. Semoga berkah.